蜜色视频-色就色综合-在线观看福利片-欧美99视频-天天看天天干-在线色网站-日韩av三区-伊人久久大香线蕉综合75-哪里有毛片看-国产女女调教女同-亚洲在线一区-亚洲少妇精品-亚洲国产成人精品久久-丰满少妇在线观看网站-99精品在线看-波多野结衣一区二

2.6 樣本統計量(統計量)(Sample Statistic)

統計圖表可方便展示資料，但對于資料的深入分析，其精確度與廣度仍不足。為了研究母體的特性(參數)，仍須用一些統計量測數，借以了解母體的特性。常用的統計量測數為代表集中趨勢統計量、代表離散統計量與形狀統計量，來表達母體的分配情形。這些樣本統計量亦稱之樣本的特征值。

2.6.1集中趨勢統計量

集中趨勢統計量是用來衡量所有觀測值聚集的中心位置---(算術)平均數、中位數、四分位數、眾數、截尾平均數

(a) 算術平均數(Arithmetic Mean)

在一般未分組的原始資料中，有n個觀測值，其集合為{x1, x2, …, xn |n?N}，則其算術平均數

=(x1 + x2 + …+ xn)/n = (xi)/n

對于分組資料，假定資料共有n個觀測值分為m組，令xi為第i組觀測值之組中點，fi為該組觀測值相對應的次數，?fi = n。則其算術平均數為

=(x1f1+x2f2+…+xmfm)/n = (xi fi)/n

 (b) 中位數(Median)

中位數又稱為二分位數，是一種由小至大順序數列的中心項。將某筆資料n個觀測值由小而大順序排列，則其中間位數的觀測值即為中位數。若n為奇數，則第(n+1)/2位數的觀測值為中位數。若n為偶數，中位數即為第n/2位數與第(n/2)+1位數觀測值的算術平均數。

(c) 四分位數(Quartile)

將觀測值由小至大順序數列按位數分為四等分，Q1 , Q2 , Q3為其位數等分點之觀測值。第0個四分位(Q0)即是最小值，第1個四分位(Q1)是第25%的值，第2個四分位(Q2)是第50%的值(即中位數)，第3個四分位(Q3)是第75%的值，第4個四分位(Q4)即是最大值。

(d) 眾數(Mode)

眾數是指統計資料中出現之次數最頻繁的觀測值。

(e) 截尾平均數(Trimmed Mean)---奧運體操評分標準

系考慮算術平均數容易受兩端特別遠離中心位置觀測值的影響，有時不能確切描述觀測值集中趨勢。即截頭去尾的方法，將Q1以下與Q3之上的觀測值排除，再計算Q1與Q3之間的觀測值的算術平均數。

2.6.2離散趨勢統計量

離散趨勢統計量是用來測量所有觀測值偏離中心的程度---全距、四分位間距、平均絕對偏差、變異數與標準差、變異系數等

(a) 全距(Range)

Range = Max. –Min.

(b) 四分位間距(IQR, Inter-Quartile Range)

四分位間距= Q3-Q1

(c) 平均絕對偏差(MAD, Mean Absolute Deviation)

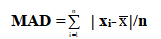
(d) 變異數與標準差(Variance and Standard Deviation)

若有N個母體觀測值{x1, x2, …, xN}，且母體平均值為m，則母體變異數為

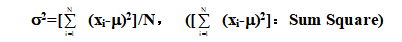
對于樣本資料{ x1, x2, …, xn}，則樣本變異數為

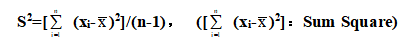
變異數是取觀測值與母體平均數差之平方和，所以變異數的單位與原觀測值所用的單位不同。為取一致可將變異數的開平方根，則s 稱之母體標準差，作為對應之離散量。另樣本標準差則相對為S。

對于分組資料，假設資料分為m組共有n個觀測值，令xi為第i組觀測值之組中點，fi為該組觀測值相對應的次數， ?fi = n。則樣本變異數為

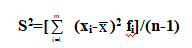
(e) 變異數系數(CV, Coefficient of Variance )

CV =(標準差/平均值)

2.6.3 形狀統計量

形狀統計量系用量測一組資料對稱與否，與分布形狀峰度之高低---分別為偏態系數與峰態系數。

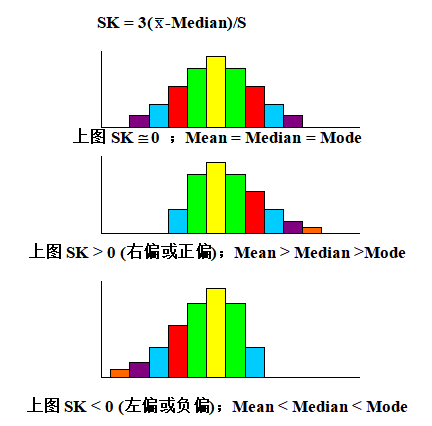
(a) 偏態系數(Skewness)

偏態系數(SK)是對資料分配偏往某一方的趨勢(Tendency)。SK的值必介于 –3與3之間。其定義

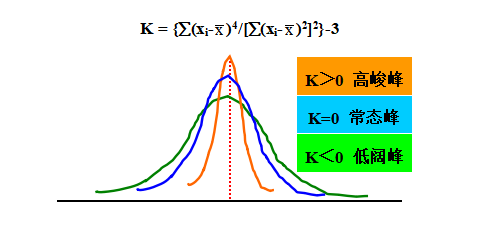
(b) 峰態系數(Kurtosis)

峰態系數(K)是對資料分配峰度(Peakedness)的程度。其定義：