摘要: SPC 即統(tǒng)計過程控制,它是利用過程的波動的統(tǒng)計規(guī)律性來對過程進(jìn)行分析控制的,其主要工具是管制圖,本文將舉例來說明如何應(yīng)用傾斜管制圖來判斷過程能否處于穩(wěn)定狀態(tài)的內(nèi)容進(jìn)行介紹.
傾斜管制圖大家可能比較陌生，它是適合應(yīng)用于產(chǎn)品作業(yè)過程中，平均值常常會自動加大或減小，如車床在加工過程中隨著數(shù)量的增加，刀具會逐漸磨損，車削外徑會逐漸增大，反之車削內(nèi)徑會逐漸變小前提需要CPK在2.0以上，如下圖：

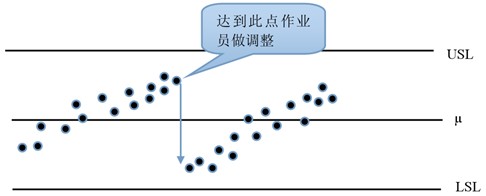
接著問題就來了：
• 作業(yè)人員什么時候調(diào)整才合理？調(diào)整過早造成不必要浪費(fèi)，過晚就有可能產(chǎn)生不良。
• 如果調(diào)整時機(jī)恰當(dāng)，那么調(diào)整到什么程度才算合理呢？很顯然當(dāng) CPK 在2.0以上時我們管制界限線線已不適用于制程管制。
    在某制程中抽取N個樣本，我們就會得到N個量測數(shù)據(jù)，計算其平均值值Xbar、樣本標(biāo)準(zhǔn)差σp，此時的X-Chart：CL=Xbar、UCL=Xbar+3σp、LCL=Xbar-3σp。
   如果我們把N個數(shù)據(jù)，分為n個一組，就會得到N/n個Xbar（分組），并計算Xdouble bar、Xbar的σ即σxbar，同樣的Xbar-chart：CL=Xdouble bar、UCL=Xdouble bar+σxbar、LCL=Xdouble bar-σxbar。在很多資料中我們都能看到這樣結(jié)論：σp= σxbar。如果假設(shè)Xdouble bar（分組）=Xbar（不分組）=µ（規(guī)格中心值）會有下圖：

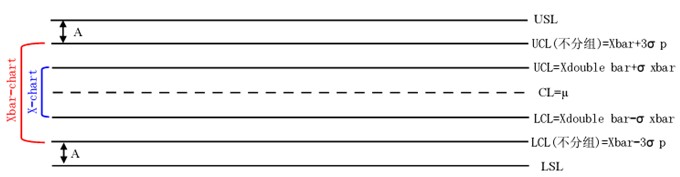
若Xbar-3σp>LSL或者說Xbar+3σp<USL，令Xbar-3σp與LSL的距離為A,實(shí)績制程中心偏移量為B，同時我們的管制上下線也會同樣偏移B的距離。以制程中心往規(guī)格下限偏移作說明：
①當(dāng)A<B時：Xbar-3σp-B<LSL，代表此時X-Chart的管制下限已經(jīng)超出規(guī)格下限；
②當(dāng)A=B時：Xbar-3σp-B=LSL，代表此時X-Chart的管制下限與規(guī)格下限重合；
③當(dāng)A>B時：Xbar-3σp-B>LSL，代表此時X-Chart的管制下限在規(guī)格下限以內(nèi)。
上述三種現(xiàn)象借用常態(tài)分配圖做進(jìn)一步說明：（僅對A=B做表述）

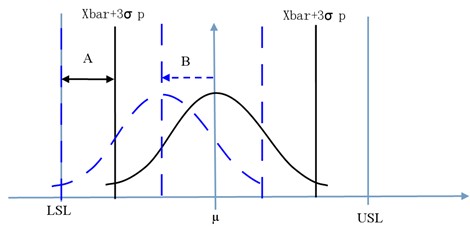
如上圖：當(dāng)A=B時，可得出此時加工制成超出規(guī)格下限的概率為：0.135%。
同樣的道理可得出：
①當(dāng)A<B時，可得出此時加工制成超出規(guī)格下限的概率>0.135%
②當(dāng)A>B時，可得出此時加工制成超出規(guī)格下限的概率<0.135%
結(jié)論：我們可根據(jù)公司要求制定制程中心的偏移范圍B，如某公司要求CPK≥1.0，那么我們就可以定A≥B即可。那么我們制程中心的總允許偏移量為2B（向上、向下偏移量），并根據(jù)制程中心的偏移量B，同樣的道理們的管制上限可向上偏移B，而管制下限可向下偏移B，如圖：

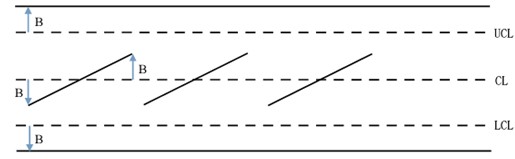
如上圖中黑實(shí)線即為傾斜管制圖中的管制線，其管制中心線為斜線，傾斜管制圖管制上限為UCL+B、管制下限為UCL-B。
實(shí)例說明：某公司要求CPK≥1.0，某零件車加工外徑規(guī)格為20.01±0.015，抽樣100個數(shù)據(jù)，已知100個樣本的標(biāo)準(zhǔn)差σp=0.003，求其制程中心可移動范圍B，及制定較為合理初始調(diào)刀加工值，需要調(diào)刀值。注：外徑車加工在刀具沒有損壞的情況下，隨時間的推移尺寸逐漸增大。
由σp=0.003推導(dǎo)LCL=20.01+3X0.003=20.019，所以A=0.006；
因公司要求CPK≥1.0，可取A=B，即B=A=0.006，所以制程中心可移動范圍為：20.01±0.006，即：此制程最理想的初始加工值為20.004，而當(dāng)制程中心隨時間推移，偏移至20.016時需作調(diào)整，此時可一次性調(diào)整0.012，調(diào)整至20.004。
追問：如果每加工100件，制程中心偏移0.006，加工多少件需調(diào)刀？
答:0.012/0.006X100=200件